Apresentação do grupo Poliedros {31-08-2016.}

Como chegar na formula de Volume da Esfera

https://www.google.com.br/url?

Poliedro Convexo

Definição

Superfície poliédrica limitada convexa é a reunião de um número finito de polígonos planos e convexos (ou regiões poligonais convexas), tais que:

•  dois polígonos não estão num mesmo plano; 
• cada lado de polígono não está em mais que dois polígonos; 
• havendo lados de polígonos que estão em um só polígono, eles devem formar uma única poligonal fechada, plana ou não, chamada contorno; 
•  o plano de cada polígono deixa os demais num mesmo semi-espaço (condição de convexidade). 

As superfícies poliédricas limitadas convexas que têm contorno são chamadas abertas. As que não tem contorno são chamadas fechadas.

Uma superfície poliédrica limitada convexa aberta ou fechada não é uma região convexa.  

Chamamos de Poliedro Convexo o polígono plano convexo (ou região poligonal convexa) com um número finito n (n 4) tal que dois polígonos não estão num mesmo plano, cada lado de polígono é comum a dois e somente dois polígonos e o plano de cada polígono deixa os demais polígonos num mesmo semi-espaço.

Nessas condições, ficam determinados n semi-espaços, cada um dos quais tem origem no plano de um polígono e contém os restantes. A intersecção desses semi-espaços é o poliedro convexo.

Elementos

Uma superfície poliédrica limitada convexa tem:

• Faces São os polígonos; 
• Arestas São os lados dos polígonos;
• Vértices São os vértices dos polígonos;
• Ângulos São os ângulos dos polígonos.
• Um poliedro convexo tem:
• Faces São os polígonos convexos;
• Arestas São os lados dos polígonos;
• Vértices São os vértices dos polígonos. 

Natureza - Poliedro Euleriano

Os poliedros para os quais vale a relação de Euler ( V – A + F = 2, onde V é o número de vértices, A é o número de arestas e F o número de faces do poliedro), são chamados poliedros eulerianos.

Todo poliedro convexo é euleriano, mas nem todo poliedro euleriano é convexo.

  

https://br.answers.yahoo.com/question/index?qid=20060912062935AAU5O5R

5 PASSOS PARA CALCULAR UM PRISMA

Prisma Triangular

1. Entenda a fórmula. Para calcular o volume de um prisma triangular use a fórmula V = (1/2 x a x l) x h, onde a representa a altura do triângulo da base do prisma, l representa o tamanho do lado do triângulo de onde foi prolongada a altura e h representa a altura do prisma.

2. Calcule a área da base do prisma. Para isso, multiplique o tamanho do lado do triângulo pelo valor da altura prolongada a partir desse lado. Em seguida, divida esse produto por dois. Vamos considerar para o exemplo que um triângulo tem altura de 5 cm e um lado de 4 cm.     Exemplo: 1/2 x a x l = 1/2 x 5 cm x 4 cm = 10 cm².
   Obtenha o valor da altura do prisma. Vamos supor para esse exemplo que a altura do prisma triangular vale 7 cm.
   Calcule o volume do prisma triangular. Finalmente, para determinar o volume desse prisma, multiplique a área calculada do triângulo de base pelo valor da altura do prisma.          Exemplo: V = (1/2 x a x l) x h = (10 cm²) x h = 10 cm² x 7 cm = 70 cm³.
   Escreva sua resposta em unidades cúbicas. Como se trata de um volume, uma grandeza tridimensional, a resposta deve ser expressa em unidades cúbicas. No exemplo, a unidade é o centímetro, logo, sua resposta final deve ser 70 cm³.

3. Obtenha o valor da altura do prisma. Vamos supor para esse exemplo que a altura do prisma triangular vale 7 cm.

4. Calcule o volume do prisma triangular. Finalmente, para determinar o volume desse prisma, multiplique a área calculada do triângulo de base pelo valor da altura do prisma. Exemplo: V = (1/2 x a x l) x h = (10 cm²) x h = 10 cm² x 7 cm = 70 cm³.
    Escreva sua resposta em unidades cúbicas. Como se trata de um volume, uma grandeza tridimensional, a resposta deve ser expressa em unidades cúbicas. No exemplo, a unidade é o centímetro, logo, sua resposta final deve ser 70 cm³.

5. Escreva sua resposta em unidades cúbicas. Como se trata de um volume, uma grandeza tridimensional, a resposta deve ser expressa em unidades cúbicas. No exemplo, a unidade é o centímetro, logo, sua resposta final deve ser 70 cm³.

Referência: http://pt.wikihow.com/Calcular-o-Volume-de-um-Prisma

PARA COMPREENDER

Os raios das bases de um tronco de cone são 6 m e 4 m. A altura referente a esse tronco é de 10 m. Determine o volume desse tronco de cone. Lembre-se que π = 3,14.

 Exemplo 2

Um tronco de cone possui a medida dos raios igual a 5 m e 8 m. Sabendo que a medida da altura é igual a 4, determine a área superficial desse sólido.

 
Para determinarmos a área superficial devemos calcular a geratriz desse tronco de cone. Observe o cálculo realizado:

 Utilizando o Teorema de Pitágoras temos:

g² = 4² + 3²
g² = 16 + 9
g² = 25
√g² = √25
g = 5

Calculando a área superficial

 

http://brasilescola.uol.com.br/matematica/tronco-cone.htm

TRONCO DE CONE

Se um cone sofrer a intersecção de um plano paralelo à sua base circular, a uma determinada altura, teremos a constituição de uma nova figura geométrica espacial denominada Tronco de Cone.

Observe que, diferentemente do cone, o tronco de cone possui duas bases circulares em que uma delas é maior que a outra, dessa forma, os cálculos envolvendo a área superficial e o volume do tronco envolverão a medida dos dois raios. 

A geratriz, que é a medida da altura lateral do cone, também está presente na composição do tronco de cone.

* Não devemos confundir a medida da altura do tronco de cone com a medida da altura de sua lateral (geratriz), pois são elementos distintos. A altura do cone forma com as bases um ângulo de 90º. No caso da geratriz os ângulos formados são um agudo e um obtuso.

h = altura
g = geratriz

As fórmulas referentes ao cálculo da área superficial e do volume são as seguintes:

Área Superficial

 Volume 

http://brasilescola.uol.com.br/matematica/tronco-cone.htm

PARA ENTENDER MELHOR!

https://youtu.be/nuA3FJMwPr4

FUSO ESFÉRICO

https://www.google.com.br/url?

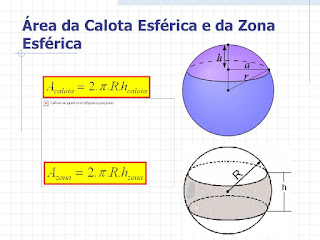
      Cilindro

      O cilindro ou cilindro circular é um sólido geométrico alongado e arredondado que possui o mesmo diâmetro ao longo de todo o comprimento.

Essa figura geométrica, que faz parte dos estudos de geometria espacial, apresenta dois círculos com raios de medidas equivalentes os quais estão situados em planos paralelos.

Componentes do Cilindro

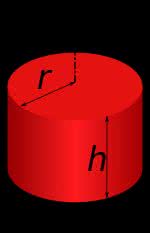
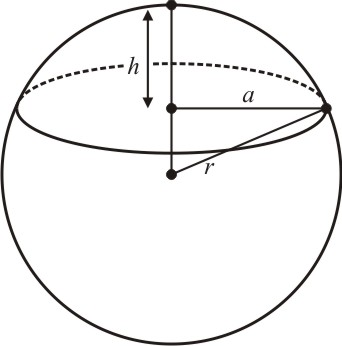
• Raio: distância entre o centro do cilindro e a extremidade.
• Base: plano que contém a diretriz e no caso dos cilindros são duas bases (superior e inferior).
• Geratriz: corresponde à altura (h=g) do cilindro.
• Diretriz: corresponde à curva do plano da base.

Classificação dos Cilindros

Dependendo da inclinação do eixo, ou seja, do ângulo formado pela geratriz, os cilindros são classificados em:

• Cilindro Reto: Nos cilindros circulares retos, a geratriz (altura) está perpendicular ao plano da base.

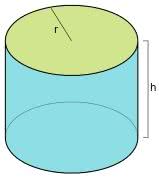
• Cilindro Oblíquo: Nos cilindros circulares oblíquos, a geratriz (altura) está oblíqua ao plano da base.

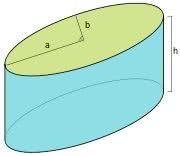
O chamado “cilindro equilátero” ou “cilindro de revolução” é caracterizado pela mesma medida do diâmetro da base e da geratriz (g=2r), uma vez que sua seção meridiana corresponde a um quadrado.

Para ampliar seus conhecimentos sobre o tema, veja outras figuras que fazem parte da Geometria Espacial.

Fórmulas do Cilindro

Segue abaixo as fórmulas para calcular as áreas e volume do cilindro:

Áreas do Cilindro

Área da Base: Para calcular a área da base do cilindro, utiliza-se a seguinte fórmula:

Ab= π.r2

Donde:

Ab: área da base
π (Pi): 3,14
r: raio

Área Lateral: Para calcular a área lateral do cilindro, ou seja, a medida da superfície lateral, utiliza-se a fórmula:

Al= 2 π.r.h

Donde:

Al: área lateral
π (Pi): 3,14
r: raio
h: altura

Área Total: Para calcular a área total do cilindro, ou seja, a medida total da superfície da figura, soma-se 2 vezes a área da base à área lateral, a saber:

At= 2.Ab+Al ou At = 2(π.r2) + 2(π.r.h)

Donde:

At: área total
Ab: área da base
Al: área lateral
π (Pi): 3,14
r: raio
h: altura

Volume do Cilindro

O volume do cilindro é calculado a partir do produto da área da base pela altura (geratriz):

V = Ab.h ou V = π.r.2h

Donde:

V: volume
Ab: área da base
π (Pi): 3,14
r: raio
h: altura

Poliedros(Exercícios resolvidos usando a Relação de Euler)

   Poliedros(Exercícios resolvidos usando a Relação de Euler) 

 

01- FATEC/SP Um poliedro convexo tem 3 faces com 4 lados, 2 faces com 3 lados e 4 faces com 5 lados. Qual é o número de vértices desse poliedro?

Solução:

Do enunciado, sabemos que

Número de faces: 3 + 2 + 4 = 9

Número de arestas:

3 faces com 4 lados: 3 . 4 = 12

2 faces com 3 lados: 2 . 3 = 6

4 faces com 5 lados: 4 . 5 = 20

Somando: 12 + 6 + 20 = 38

Atenção:As faces são unidas, duas a duas, por uma aresta. Ao contarmos todas as arestas de todas as faces, cada aresta é contada duas vezes, uma para cada face "grudada" nela. Assim, esse número, na verdade, é o dobro do número real de arestas do poliedro. Logo:

A = 38 ÷ 2 = 19.

Usando, agora, a Relação de Euler, temos:

V + F = 2 + A

V + 9 = 2 + 19

V = 21 - 9  ► V =  12.

02.Num poliedro convexo, o número de faces é 8 e o número de arestas é 12. Qual é o número de vértices desse poliedro?

Solução:

Usando a relação de Euler, temos:

V + F = A + 2

V + 8 = 12 + 2

 V = 6

 

03.Um poliedro convexo possui 2 faces triangulares e 3 faces quadrangulares.Determine o número de arestas e de vértices desse poliedro.

Solução:

Número de arestas 18 arestas

2 faces triangulares ►2 x 3 = 6

                              

3 faces quadrangulares ►3 x 4 = 12

Uma aresta é comum a 2 faces, então

2A = 18 ► A = 9.

Número de vértices:

V + F = A + 2 F = 2 + 3

V + 5 = 9 + 2 F = 5

V = 11 – 5   ►  V = 6

http://cantinhodocalazans.blogspot.com.br/2013/09/poliedrosexercicios-resolvidos-usando.html

Volume do segmento Esfèrico

https://youtu.be/b_uHA29L9Tk

Geometria Espacial - Aula 3 - Cilindros - Prof. Gui

    https://www.youtube.com/watch?v=GZ5p4WdWa2o

Volume de pirâmide - Parte 1 - Aula 21

https://www.youtube.com/watch?v=SSW2h6PJUeA&index=19&list=PL7RjLI0hJPfAUKfDRxobMe0CzjIOccXqZ#t=34.952122

VOLUME DA PIRAMIDE

Dado um polígono contido num plano e um ponto V fora desse plano, define-se pirâmide como sendo a reunião de todos os segmentos com uma extremidade em V e a outra num ponto qualquer do polígono. O ponto V é chamado de vértice da pirâmide.

As pirâmides são classificadas de acordo com a forma de sua base. Além do vértice da pirâmide podemos destacar outros elementos importantes como: a altura, o apótema, a superfície lateral e, claro, a base.

O volume de uma pirâmide é dado em função da área de sua base e da altura h, de acordo com a fórmula abaixo:

Onde

V → é o volume
A_b → é a área da base da pirâmide
h → é a altura da pirâmide

Exemplo 1. Calcule o volume da pirâmide de base quadrada a seguir:

Solução: Pela análise da figura, temos que:

h = 9 cm
A_b = 6² = 36 cm²

Assim, o volume da pirâmide será dado por:

Exemplo 2. Calcule o volume de uma pirâmide regular de base hexagonal sabendo que sua altura é de 12 cm e que cada aresta da base mede 8 cm.

Solução: Primeiro, vamos calcular a área da base dessa pirâmide. Sabemos que a base da pirâmide é um hexágono regular de 8 cm de aresta. A área do hexágono regular é dada por:

Conhecida a medida da área da base da pirâmide, podemos utilizar a fórmula do volume.

http://brasilescola.uol.com.br/matematica/volume-piramide.htm

Poliedros de Kepler-Poinsot 

 

https://www.google.com.br/search?q=poliedros+resumo&biw=1366&bih=657&source=lnms&tbm=isch&sa=X&sqi=2&ved=0ahUKEwiHyfzhwsTOAhXCjJAKHQvUAXwQ_AUIBigB#imgrc=s5MinnwRiUtlVM%3A

Área de uma calota Esferica

Formula da Calota

https://www.google.com.br/imgres?

Volume de uma Calota Esfèrica

Para esta demonstração, podemos partir do mesmo princípio utilizado para o cálculo do Volume da Esfera, envolvendo o conceito de integral definida. Podemos adotar o mesmo raciocínio para encontrarmos a função f (x) a ser integrada, alterando somente os limites de integração.

Primeiramente, vamos definir: Calota esférica é o sólido gerado a partir de uma esfera ao ser seccionada por um plano:

[Figura 1]

Desta forma, os limites de integração serão de r – h até r.

Para simplificar este desenvolvimento, vamos partir da função f (x), que foi originada da equação da circunferência de centro na origem:

Veja o desenvolvimento completo acessando o link para o Volume da Esfera.

Vamos posicionar a figura 1 de outro modo, mais conveniente:

[Figura 2]

Suponha, agora, a calota esférica de altura h formada por infinitos cilindros de alturas infinitesimais dx e raios y, onde y é variável para cada ponto de h:

[Figura 3]

Sabemos que o volume do cilindro é dado por:

E, neste caso:

A soma destes infinitos cilindros de alturas infinitesimais forma a calota esférica, nos limites r – h e r. Então, o seu volume será dado por:

Substituímos a equação (1) na integral (3):

Integrando em relação a x, obtemos:

Aplicamos os limites:

Agora é somente álgebra:

http://obaricentrodamente.blogspot.com.br/2010/09/volume-de-uma-calota-esferica.html